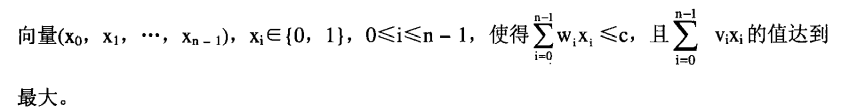一、贪心算法
1、何为贪心:
贪心算法或贪心思想采用贪心的策略,保证每次操作都是局部最优的,从而使最后得到的结果是全局最优的。
2、背包问题/分配问题:

题解:先填小的,再添大的
3、区间问题:

二、双指针法
双指针主要用于遍历数组,两个指针指向不同的元素,从而协同完成任务。也可以延伸到多个数组的多个指针。
若两个指针指向同一数组,遍历方向相同且不会相交,则也称为滑动窗口(两个指针包围的区域即为当前的窗口),经常用于区间搜索。
若两个指针指向同一数组,但是遍历方向相反,则可以用来进行搜索,待搜索的数组往往是排好序的。
1、例1:

题解:反向
2、归并两个有序数组:

初始思路:
从两个数组自前向后比较大小,优先输出小的,输出之后滑动一位。
标准题解:

3、快慢指针找环路:

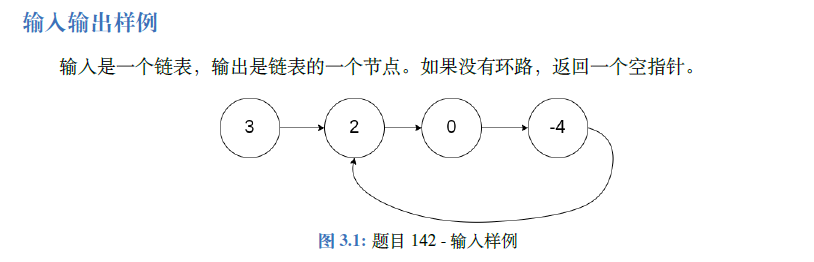
题解:
快慢指针(Floyd 判圈法)。
给定两个指针,分别命名为slow 和fast,起始位置在链表的开头。
每次 fast 前进两步,slow 前进一步。
如果fast可以走到尽头,那么说明没有环路;
如果fast 可以无限走下去,那么说明一定有环路,且一定存在一个时刻slow 和fast 相遇。
当slow 和fast 第一次相遇时,我们将fast 重新移动到链表开头,并让slow 和fast 每次都前进一步。
当slow 和fast 第二次相遇时,相遇的节点即为环路的开始点
4、滑动窗口:
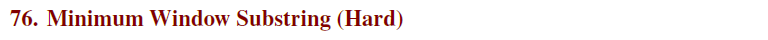

题解:略
三、动态规划(Dynamic Programming, DP)
Wiki对动态规划的定义:
动态规划(英语:Dynamic programming,简称DP)是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的,通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。
动态规划常常适用于有重叠子问题[1]和最优子结构性质的问题,动态规划方法所耗时间往往远少于朴素解法。
最优子结构的意思是局部最优解能决定全局最优解(对有些问题这个要求并不能完全满足,故有时需要引入一定的近似),简单地说,问题能够分解成子问题来解决。
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:
一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。
这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。即,动态规划保存递归时的结果,因而不会在解决同样的问题时花费时间。
应用实例:
切割钢条问题;Floyd最短路问题;最大不下降子序列;矩阵链乘;凸多边形三角剖分;0-1背包;最长公共子序列;最优二分搜索树;
小结:
动态规划和其它遍历算法(如深/广度优先搜索)都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存子问题的解,避免重复计算。
解决动态规划问题的关键是找到状态转移方程,这样我们可以通过计算和储存子问题的解来求解最终问题。同时,我们也可以对动态规划进行空间压缩,起到节省空间消耗的效果。
例题:LeetCode(题解放置本节后,留作回顾思考)

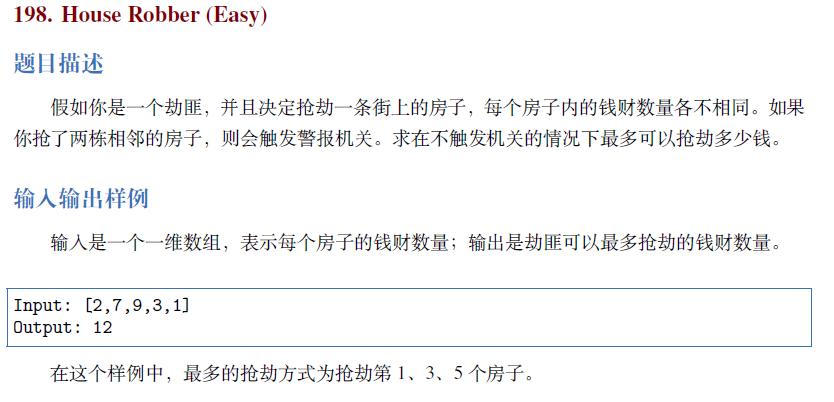

更多例题,日后继续扩展
可参考高畅大神的《A LeetCode Grinding Guide》一书
以下为题解:




另:背包问题
基本概念:
背包问题是一种组合优化的 NP 完全问题:
有 N 个物品和容量为 W 的背包,每个物品都有自己的体积 w 和价值 v,求拿哪些物品可以使得背包所装下物品的总价值最大。
如果限定每种物品只能选择 0 个或 1 个,则问题称为 0-1 背包问题;
如果不限定每种物品的数量,则问题称为无界背包问题或完全背包问题。
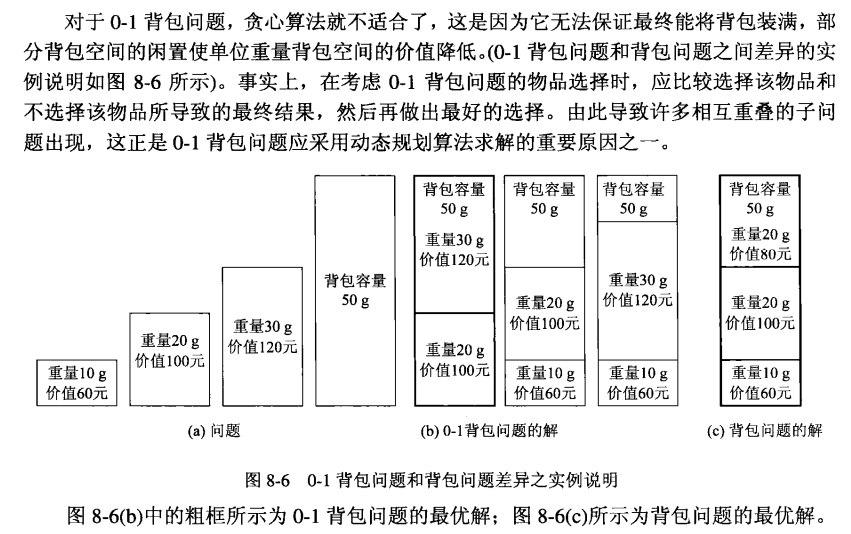
XDU课本中对背包问题的描述: