ASL:平均查找长度 如图:p:查找到该元素的概率 c:比较次数
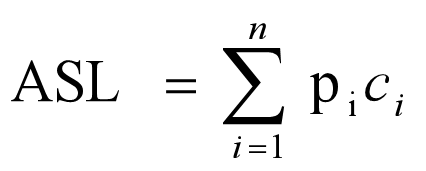
一、静态查找
1、顺序查找
习惯性选择从后往前查找
(1)无序表:
主要引入监视哨概念(copy的代码如下)
#include<iostream>
#include<cstdio>
#include<cstdlib>
using namespace std;
typedef struct{
KeyType key;
OtherInfoType info;
}ElemType;
typedef struct{
ElemType *elem;//数据元素存储空间基址,建表时,按实际长度分配,0号单元留空
int length;//表长
}SSTable;
//在无序表中查找元素key所在的位置,查找成功则返回元素在表中的位置,否则返回0
int Sq_search(SSTable ST,KeyType key){
int i=ST.length;
ST.elem[0].key=key;//监视哨:下标为0的位置存放待查找的元素
while(ST.elem[i].key!=key) i--;
return i;
}
int main(){
return 0;
}
将0号单元设置为“监视哨” 的目的是使得代码内的循环不必判断数组是否会越界,因为满足i==0时,循环一定会跳出,从而减少不必要的循环语句,进而提高程序效率。
ASL_成功 = (n+1)/2
ASL_失败 = n+1
(2)有序表:
ASL_成功 = (n+1)/2
ASL_失败 = (n+2)/2
2、折半查找(前提:有序表)
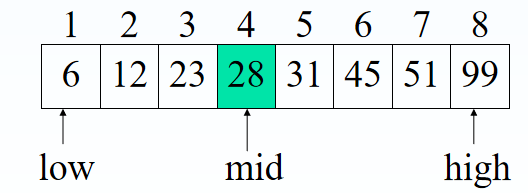
mid = ( low + high ) / 2 注:向下取整
算法思想:
先确定待查记录所在的范围(区间),若待查记录等于表中间位置上的记录,则查找成功;否则,缩小查找范围,即若待查记录小于中间位置上的元素,则下一次到前半区间进行查找,若待查记录大于中间位置上的元素,则下一次到后半区间进行查找。
注:链表只能顺序查找,因为不能随机存取
实战例子:LeetCode #35 搜索插入位置

题解:
class Solution
{
public:
int searchInsert(vector<int>& nums, int target)
{
int n = nums.size();
int L = 0, R = n-1;
int mid;
while(L <= R)
{
mid = (L + R)/2;
if(target > nums[mid]) L++;
else R--;
}
return L;
}
};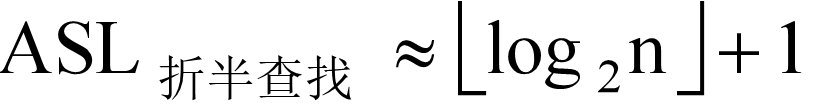
3、分块查找(索引查找)
分块查找要求把数据分为若干块,每一块里面的元素可以是无序的,但是块与块之间的元素需要是有序的。
同时,分块查找需要一个索引表,用来限定每一块的范围,在增加、删除、查找元素时都需要用到。
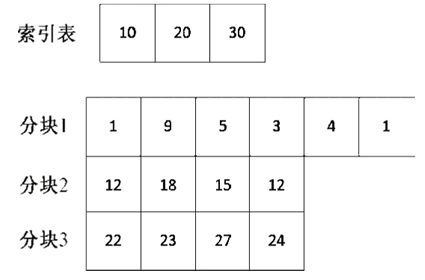
如果要查找图 1 中的 27 这个数,则首先该怎么做呢?通过二分查找索引表,我们发现 27 在分块 3 里,然后在分块 3 中顺序查找,得到 27 存在于数列中。
分块查找的特点:
分块查找拥有顺序查找和二分查找的双重优势,即顺序查找不需要有序,二分查找的速度快。
二、动态查找(可以增删改查)
二叉排序树:
- 若其左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若其右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 其左、右子树也分别为二叉排序树;
查找算法:
BiTree SearchBST(BiTree T,keyType key) {
//在T指向根的二叉排序树中递归地查找关键字等于key的数据元素,
//若找到,返回指向该结点的指针,否则返回NULL
if (T==NULL) return NULL;
else if (T->data.key==key) return T;
else if (key < T->data.key)
return SearchBST(T->lchild,key);
else return SearchBST(T->rchild,key);
}
二叉排序树的创建构造:
若二叉排序树为空树,则插入元素作为树根结点;
若根结点的键值等于key,则插入失败;
若key小于根结点的键值,则插入到根的左子树上;否则,插入到根的右子树上;
新插入的结点一定是个叶子结点;
二叉排序树结点的值一定是唯一的;且插入的新值,一定是插入在为空的位置上;
二叉排序树的查找性能:
求ASL和二分的查找树一样,若查找成功,则走了一条从根结点到某结点的路径,若查找失败,则走到一棵空的子树时为止。因此,最坏情况下,其平均查找长度不会超过树的高度。高度越高平均查找长度就越大。
二叉平衡树:
旋转问题-待更新…
三、哈希表
1、定义:
散列:也称为杂凑或哈希。它既是一种查找方法,又是一种存储方法,称为散列存储,其内存存放形式也称为哈希表或散列表。
一般情况下,设计出的散列函数很难是单射的,即不同的关键字对应到同一个存储位置,这样就造成了冲突(碰撞)。此时,发生冲突的关键字互为同义词
2、散列函数的构造方法
直接定址法、数字分析法、平方取中法、折叠法、随机数法、除留余数法
3、解决冲突的方法
(1)开放定址法
开放定址法就是从发生冲突的那个单元开始,按照一定的次序,从哈希表中找出一个空闲的存储单元,把发生冲突的待插入关键字存储到该单元中,从而解决冲突。
a. 线性探测
线性探测再散列法充分利用了哈希表的空间,但在解决一个冲突时,可能造成新的冲突(聚集)。另外,也不能随便对结点进行删除。
(2)拉链法


