一、基础知识:
1、MNIST数据集
本实验采用的数据集MNIST是一个手写数字图片数据集,共包含图像和对应的标签。数据集中所有图片都是28×28像素大小,且所有的图像都经过了适当的处理使得数字位于图片的中心位置。MNIST数据集使用二进制方式存储。图片数据中每个图片为一个长度为784(28x28x1,即长宽28像素的单通道灰度图)的一维向量,而标签数据中每个标签均为长度为10的一维向量。
2、分层采样方法
分层采样(或分层抽样,也叫类型抽样)方法,是将总体样本分成多个类别,再分别在每个类别中进行采样的方法。通过划分类别,采样出的样本的类型分布和总体样本相似,并且更具有代表性。在本实验中,MNIST数据集为手写数字集,有0~9共10种数字,进行分层采样时先将数据集按数字分为10类,再按同样的方式分别进行采样。
3、神经网络模型评估方法
通常,我们可以通过实验测试来对神经网络模型的误差进行评估。为此,需要使用一个测试集来测试模型对新样本的判别能力,然后以此测试集上的测试误差作为误差的近似值。两种常见的划分训练集和测试集的方法:
留出法(hold-out)直接将数据集按比例划分为两个互斥的集合。划分时为尽可能保持数据分布的一致性,可以采用分层采样(stratified sampling)的方式,使得训练集和测试集中的类别比例尽可能相似。需要注意的是,测试集在整个数据集上的分布如果不够均匀还可能引入额外的偏差,所以单次使用留出法得到的估计结果往往不够稳定可靠。在使用留出法时,一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
k折交叉验证法(k-fold cross validation)先将数据集划分为k个大小相似的互斥子集,每个子集都尽可能保持数据分布的一致性,即也采用分层采样(stratified sampling)的方法。然后,每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集,这样就可以获得k组训练集和测试集,从而可以进行k次训练和测试。最终返回的是这k个测试结果的均值。显然,k折交叉验证法的评估结果的稳定性和保真性在很大程度上取决于k的取值。k最常用的取值是10,此外常用的取值还有5、20等。
二、python实现
1、神经网络模型构建的程序设计

这里我们由于要满足97%以上,因此人工神经网络的层数可能要相对多一些,仅仅一个隐藏层是没有办法达到的,为此我们为了方便,选择建立一个全连接层(FCN)函数,方便之后调用。
接下来这里开始构建我们的人工神经网络结构:隐藏层为2层,神经元分别为256和64,激活函数选择的是relu,我们的损失函数采用交叉熵。
交叉熵损失函数是刻画的是两个概率分布之间的距离,交叉熵越小,两个概率的分布越接近。
(Tips:关于激活函数的选择,没有选择sigmoid的原因是他的导数不能满足MINIST)

2、模型迭代训练的程序设计
模型迭代40轮,每轮全部数据集,但是按每批次50个样本进行训练,这里迭代训练采用了原码中batch_iter函数,因此我在hold_on和k_fold中所分割的训练集和测试集需要有一一对应关系,按照标签分布。
3、两种采样方式的程序设计
由于我们是探究两种不同采样方式对准确率的影响,因此其实这一部分的实现过程无论是自己造轮子还是采用现有的库都无所谓。众所周知python的sklearn库里有很多喜闻乐见的工具,其中自然包括这两种采样方式:
HoldOn:

Tips:
random_state=1可确保每次得到相同的分割,以便再现结果
stratify=y,则表示进行分层抽样
K-Fold:

- 实验结果展示
1、模型在验证集下的准确率
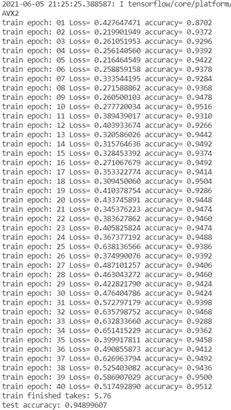

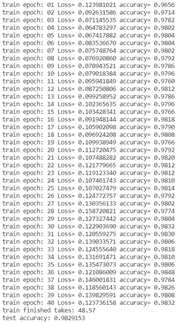
数据说明:左图为holdon三层,右图为Kfold两层,我们根据之后的针对网络结构的分析得知,层数越少(一定范围内),准确率会越高,我们也可以分析出来,两种采样方式对于模型的准确率有着不小的差别,K-fold显著强于HoldOn。
2、不同模型参数对准确率的影响和分析
(KFold为例)
设计方式:




层数还是有一定影响的,层数越多准确率能高一些。
至于神经元,如果神经元越多,我们训练的时间就会越长,而准确率会有一定提升,但是如果超出一定量,易造成过拟合。
3、不同训练参数对准确率的影响和分析

这是我们默认的超参数设置
下面对各个参数进行一定的解释:
训练轮数和单次样本数现在的数值已经相对比较好,当然小小的增加似乎可以提升一点,但是很多时候用处不明显。
显示粒度对于模型没有用处,只是输出结果的形式。
学习率越低,对于模型的准确率越高。
4、留出法不同比例对结果的影响和分析
训练数据越少,准确率越差。这个毋庸置疑。
5、k折交叉验证法不同k值对结果的影响和分析
K越大,准确率越高(但是效率太低);双层下:5和20对比

最后:
先找,再造轮子…



